O que é a Teoria BCS?
A teoria BCS foi desenvolvida e explicada por John Bardeen, Leon Cooper e John Robert Schrieffer.
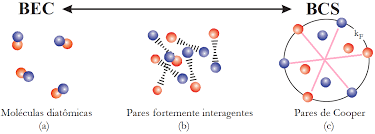
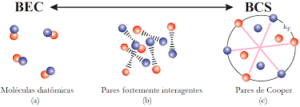
Ele afirma principalmente que os elétrons em um estado supercondutor em um material se reúnem em pares chamados pares de Cooper. Os pares de Cooper são elétrons que se condensam em estados de energia mais baixos. A formação dos pares de Cooper depende da microestrutura do material, do formato da rede, pois o par de elétrons se move de forma que é acoplado à rede.
Nikolay Bogoliubov explicou de forma independente e simultânea esse fenômeno de supercondutividade através da chamada transformação de Bogoliubov.
Em muitos supercondutores, interações atrativas entre elétrons (que devem ser pareados) são conduzidas aproximadamente e indiretamente por interações entre elétrons e estruturas cristalinas vibrantes (fônons).
Os elétrons que passam pelo condutor atrairão cargas positivas próximas à estrutura. A deformação dessa estrutura faz com que outro elétron com spin oposto se mova em uma região de maior densidade de carga positiva. Os dois elétrons são então mantidos juntos com alguma energia de ligação. Se essa energia de ligação for maior que a energia fornecida pelo pulso gerado pela oscilação dos átomos no condutor (que se encontra em baixas temperaturas), então o par de elétrons ficará junto e resistirá ao pulso, sem resistência.
A teoria do BCS foi proposta em 1957 por John Bardeen, Leon Cooper e Robert Schrieffer, pelo qual ganhou o Prêmio Nobel de Física em 1972.
Em 1986, foi descoberta a “supercondutividade de alta temperatura” (ou seja, supercondutividade em temperaturas bem acima do limite anterior de cerca de 30 K; acima de cerca de 130 K). Acredita-se que outros efeitos estão em jogo nessas temperaturas. Esses efeitos não são totalmente compreendidos. (Para alguns materiais, esses efeitos desconhecidos podem igualmente governar a supercondutividade, mesmo em baixas temperaturas.)
A teoria BCS começa com a suposição de que existe uma certa força atrativa entre os elétrons que pode exceder a repulsão de Coulomb. Na maioria dos materiais (em supercondutores de baixa temperatura), essa atração ocorre aproximadamente indiretamente através do acoplamento de elétrons à estrutura cristalina (como descrito acima). No entanto, os resultados da teoria BCS não dependem da origem da interação atrativa. Os resultados iniciais do BCS (discutidos abaixo) descrevem o estado supercondutor de onda s, que é a regra em supercondutores de baixa temperatura, mas não realizado em muitos “supercondutores não convencionais”, como supercondutores de alta temperatura de “onda d”. Extensões da teoria BCS existem para descrever esses outros casos, embora sejam insuficientes para descrever completamente as propriedades observadas da supercondutividade de alta temperatura.
BCS pode dar uma aproximação do estado da mecânica quântica de sistemas eletrônicos (interações atrativas) dentro de metais. Este estado é agora referido como o “estado BCS”. No estado normal do metal, os elétrons se movem independentemente, enquanto no estado BCS eles estão conectados em “pares Cooper” por meio de interações atrativas.
O BCS produziu várias previsões teóricas importantes que são independentes dos detalhes da interação, pois as previsões quantitativas mencionadas abaixo valem para qualquer atração suficientemente fraca entre elétrons e para muitos supercondutores de baixa temperatura – o chamado “por exemplo, acoplamento fraco”. Estes foram confirmados em muitos experimentos:
Como os elétrons estão ligados em pares de Cooper, é necessária uma quantidade finita de energia para quebrá-los em dois elétrons separados. Isso significa que há uma “abertura (janela) de energia” para “excitação de partícula única”, ao contrário dos metais comuns (onde o estado de um elétron pode ser alterado pela adição de uma pequena quantidade arbitrária de energia). Essa lacuna de energia é maior em baixas temperaturas, mas desaparece na temperatura de transição, onde a supercondutividade está ausente. A teoria BCS prevê corretamente essa abertura em função da temperatura. Novamente, dá uma expressão mostrando como o tamanho dos poros cresce com a força da interação atrativa e a densidade de partículas (normal) do estado de energia de Fermi. Além disso, descreve como a densidade de estados pode ser alterada para incluir estados supercondutores, onde não há estados eletrônicos na energia de Fermi. A diferença de energia é observada mais diretamente em experimentos de tunelamento e reflexões de micro-ondas supercondutoras.